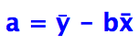Regression
In GCSE you draw a line of best fit.
Regression enables this line to be mathematically worked out
Regression enables this line to be mathematically worked out
Line of Best Fit
For a regression line of bivariate data the equation is y = a + bx (same thing as y = mx + c except values are switched)
b is the gradient
b = Sxy
Sxx
a is the y intercept
b is the gradient
b = Sxy
Sxx
a is the y intercept
Coding
In coding the regression line may not be the same.
In an exam you may be asked to find the regression line equation for the coded data
E.g.
If you've discovered the regression line is y = 36 - 5x
and the coding was x = 10c and y = 2 + m
Substitute these values in
Giving
2 + m = 36 - 5(10c)
use algebra to discover the coded line is
m = 34 - 50c
In an exam you may be asked to find the regression line equation for the coded data
E.g.
If you've discovered the regression line is y = 36 - 5x
and the coding was x = 10c and y = 2 + m
Substitute these values in
Giving
2 + m = 36 - 5(10c)
use algebra to discover the coded line is
m = 34 - 50c
Interpolation and Extrapolation
Interpolation - estimate value within data range
Extrapolation - estimate value out of data range
You do this by using the regression line and substituting in x and y values
The more you extrapolate the less reliable the result is as the data may follow a different trend out of the range collected
Extrapolation - estimate value out of data range
You do this by using the regression line and substituting in x and y values
The more you extrapolate the less reliable the result is as the data may follow a different trend out of the range collected