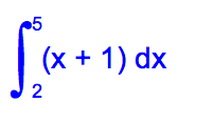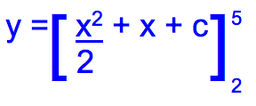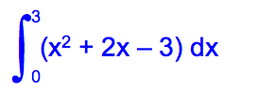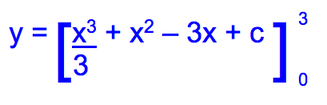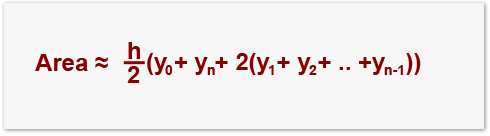Integration
Definite Integration
When given two x co-ordinates (limits) you can use definite integration to give the area between the line and the x axis
The 5 and 2 are the x limits
This integrates to:
This integrates to:
Substitute in the x values giving:
y = 17.5 + c and y = 4 + c
To find the area subtract the larger area from the smaller one:
(17.5 + c) - (4 + c) = 13.5 ('c's cancel out)
Generally give the result as fractions so to give the exact area
y = 17.5 + c and y = 4 + c
To find the area subtract the larger area from the smaller one:
(17.5 + c) - (4 + c) = 13.5 ('c's cancel out)
Generally give the result as fractions so to give the exact area
|
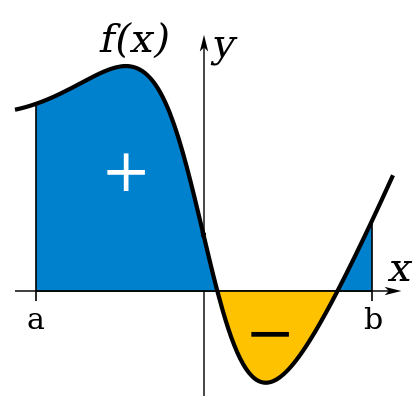
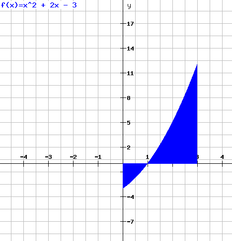
There is a TRAP!
Some integrals may go below the x axis. When this occurs the integral produces a negative result.
This is a problem as this means that instead of adding the two areas from either side of the x axis, you are subtracting one from another. To avoid this draw out the graph. Find out the x intercept. Find out the integrals on either side and add them together to find the area. |
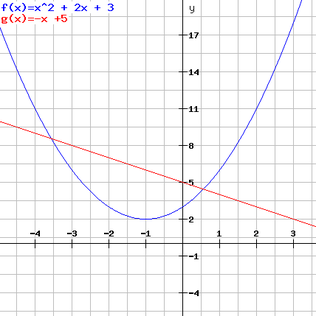
You also need to be able to find the area between a curve and a straight line.
The limits are where the two lines meet. Find this by putting the two equations equal to each other.
Find the two areas using integration between the two limits (the trap still affects this result) and then minus one area from the other depending on which graph goes furthest away from the x axis within the limits
The limits are where the two lines meet. Find this by putting the two equations equal to each other.
Find the two areas using integration between the two limits (the trap still affects this result) and then minus one area from the other depending on which graph goes furthest away from the x axis within the limits
Trapezium Rule
h = width of a strip
y0 = first y value
yn = last value
y0 = first y value
yn = last value
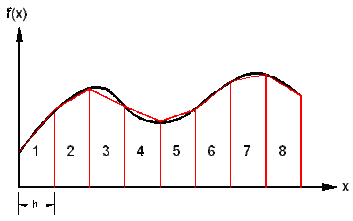
The Trapezium Rule takes a strip of a certain width and assumes that the two points it meets the line forms a trapezium. This rule then works out the sum of the areas of these trapeziums. This is why there is the '≈' as this means that this is an approximate area. If you do the integral of the line it would show a similarity to the trapezium rule but they wouldn't be the same values. The thinner the strips are the closer the trapezium rule gets to the actual area.
In an exam a table of values will be given that can be used to find out the parts of the equation.
This is on the equation sheet
This is on the equation sheet