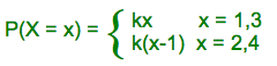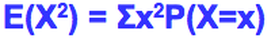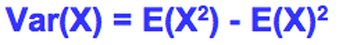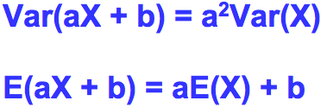Discrete Random Variables
A variable is represented by a capital letter i.e. X
This can be any particular x value
A discrete random variable can only be certain discrete values
P(X = x) is the probability that the random variable is the same as a particular value of x
You will be given P(X = x) in an exam
This can be any particular x value
A discrete random variable can only be certain discrete values
P(X = x) is the probability that the random variable is the same as a particular value of x
You will be given P(X = x) in an exam
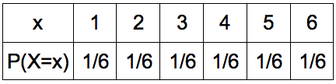
Probability Distribution
A probability distribution is a table like above
REMEMBER that it's probability, so ΣP(X=x) = 1
REMEMBER that it's probability, so ΣP(X=x) = 1
What if:
Here there are two different probabilities and a constant
So k + 3k + (2-1)k + (4-1)k = 1
8k = 1
k = 1/8
So k + 3k + (2-1)k + (4-1)k = 1
8k = 1
k = 1/8
What if:
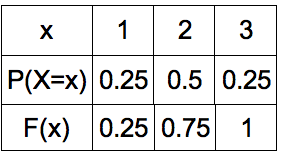
P(1 < X < 5)
This is the same as P(X = 2,3 or 4)
P(X = 2) = 0.2
P(X = 3) = 0.3
P(X = 4) = 0.25
P(1 < X < 5) = 0.75
P(1 < X < 5)
This is the same as P(X = 2,3 or 4)
P(X = 2) = 0.2
P(X = 3) = 0.3
P(X = 4) = 0.25
P(1 < X < 5) = 0.75
Cumulative Distribution Function
Mean / Expected Value and Variance
This gives the mean of the data
E(X) = ΣxP(X=x)
Using this formula means to multiply each P(X = x) by the corresponding x value and find the sum of these
This gives the mean of the data squared
This gives the mean of the data squared
To find the Variance of the data
These can be translated:
You need to remember these
You need to remember these
Coding
During coding of bivariate data the variables are coded
E.g.
Y = X - 150 with standard deviation of 2.5 and the variable Y mean being 5.1
50
To find E(X)
Rearrange to X = 50Y + 150
This means E(X) = E(50Y + 150)
Using your transformation laws
E(X) = 50E(Y) + 150
E(X) = 50 x 5.1 + 150
E(X) = 406
Finding the variance is similar
E.g.
Y = X - 150 with standard deviation of 2.5 and the variable Y mean being 5.1
50
To find E(X)
Rearrange to X = 50Y + 150
This means E(X) = E(50Y + 150)
Using your transformation laws
E(X) = 50E(Y) + 150
E(X) = 50 x 5.1 + 150
E(X) = 406
Finding the variance is similar
Modeling
When you have a discrete uniform distribution, where the probability for every X value is the same, you can create a model which allows you to work out the mean and variance of X values up to an unknown amount (n)
So when x = 1,2,3... n
Then P(X=x) = 1/n
For this
E(X) = n + 1
2
Var(X) = (n + 1)(n - 1)
12
So when x = 1,2,3... n
Then P(X=x) = 1/n
For this
E(X) = n + 1
2
Var(X) = (n + 1)(n - 1)
12