Probability
Don't use percentages use fractions or decimals
Symbols
P(?) - Probability of
∪ - Or
∩ - and
A - Variable
A' - not A
P(A|B) - Probability of A given B
Mutually Exclusive - Events that can't occur at the same time. Penny flipped twice
Conditional - Events that occur because of the other or at the same time. Penny and Dice rolled same time
∪ - Or
∩ - and
A - Variable
A' - not A
P(A|B) - Probability of A given B
Mutually Exclusive - Events that can't occur at the same time. Penny flipped twice
Conditional - Events that occur because of the other or at the same time. Penny and Dice rolled same time
Probability Relationships
Addition Rule
Mutually Exclusive - P(A ∪ B) = P(A) + (B)
Conditional - P(A ∪ B) = P(A) + P(B) - P(A ∩ B) - in formula booklet
Multiplication Rule
Mutually Exclusive - P(A ∩ B) = P(A) x P(B)
Conditional - P(A ∩ B) = P(A) x P(B|A) - in formula booklet
When an event is mutually exclusive - P(A and B) = 0
Only the conditional rules are in the formula booklet
Mutually Exclusive - P(A ∪ B) = P(A) + (B)
Conditional - P(A ∪ B) = P(A) + P(B) - P(A ∩ B) - in formula booklet
Multiplication Rule
Mutually Exclusive - P(A ∩ B) = P(A) x P(B)
Conditional - P(A ∩ B) = P(A) x P(B|A) - in formula booklet
When an event is mutually exclusive - P(A and B) = 0
Only the conditional rules are in the formula booklet
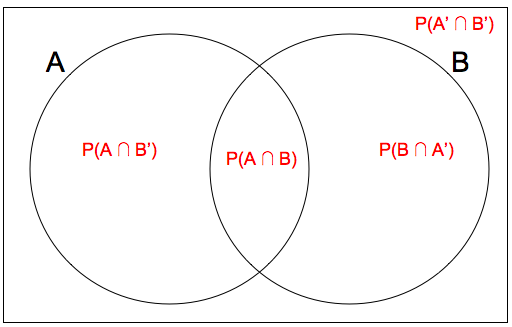
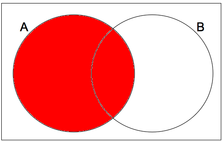
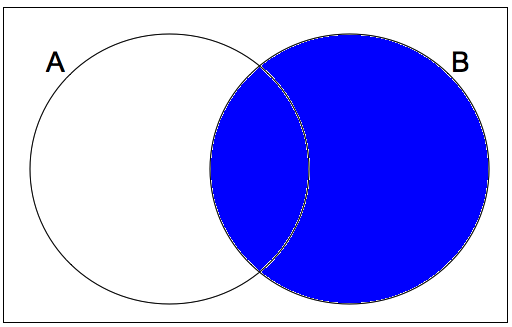
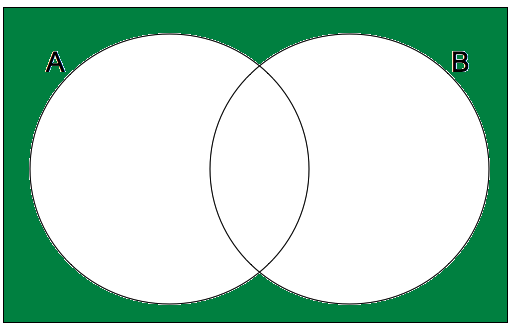
Venn Diagram
Venn diagrams plot probability values
Below is which values go where
Below is which values go where
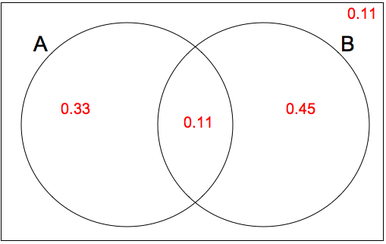
If given values P(A ∪ B) = 0.89, P(A ∩ B) = 0.33 and P(A ∩ B) = 0.45
The venn diagram will be
The venn diagram will be
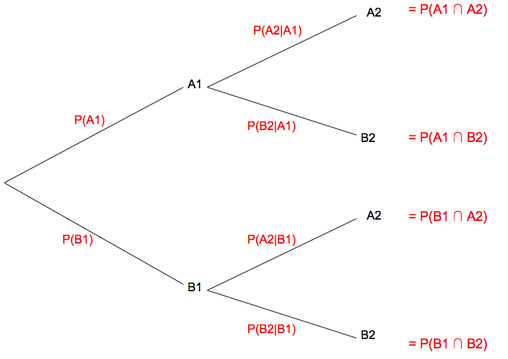
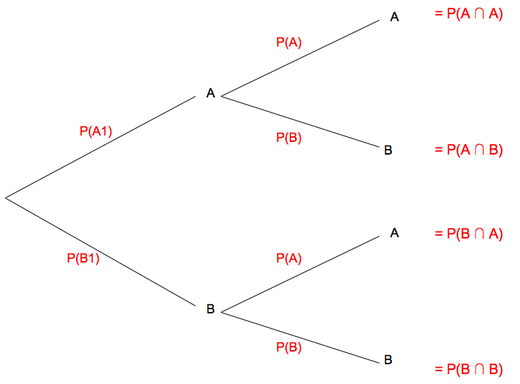
Tree Diagram
Going across branches - multiply
Going down branches - addition
Going down branches - addition
Conditional Variables
This is when the first occurence occurs and then the second occurrence happens due to or because of the first occurrence
E.g.
There is a bag of counters labelled A and B. A counter is chosen and not replaced. Another counter is chosen.
The second choice's probability is different due to a counter being removed
Exam question:
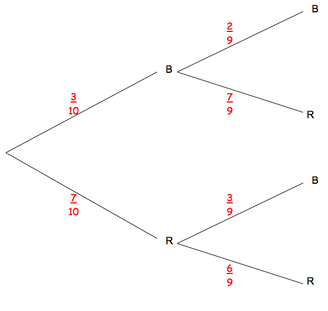
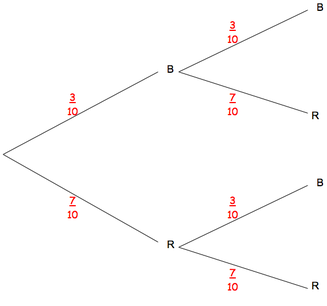
Bag of 10 counters, 3 blue and 7 red. One counter is chosen at random but not replaced. Another counter is chosen. Draw a labelled tree diagram to represent this data.
E.g.
There is a bag of counters labelled A and B. A counter is chosen and not replaced. Another counter is chosen.
The second choice's probability is different due to a counter being removed
Exam question:
Bag of 10 counters, 3 blue and 7 red. One counter is chosen at random but not replaced. Another counter is chosen. Draw a labelled tree diagram to represent this data.
Mutually Exclusive / Independent Variables
This is when the first and second occurrences happen independently from each other
E.g.
There is a bag of counters of A and B. A counter is chosen and put back. Another counter is chosen.
The second choice's probability is the same
Exam Question:
Bag of 10 counters, 3 are red and 7 are blue. One counter is chosen at random and replaced. Another counter is chosen. Draw a labelled tree diagram to represent this
E.g.
There is a bag of counters of A and B. A counter is chosen and put back. Another counter is chosen.
The second choice's probability is the same
Exam Question:
Bag of 10 counters, 3 are red and 7 are blue. One counter is chosen at random and replaced. Another counter is chosen. Draw a labelled tree diagram to represent this