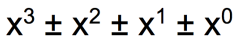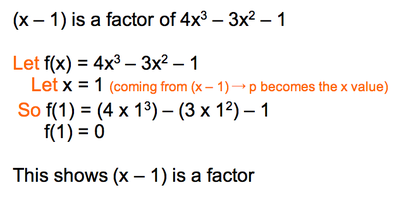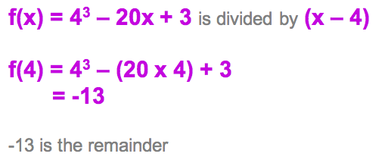Algebra and Functions
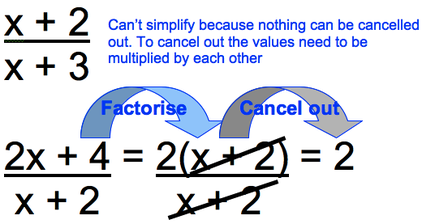
Simplifying algebraic fractions
Dividing polynomials by (x ± p)
The key here is to remember how to use long division all the way back in primary school!!
A polynomial is a set of positive powers in order
A polynomial is a set of positive powers in order
|
If you can't follow the diagram this video takes you through the process step by step - http://www.youtube.com/watch?v=qIpCI2iKbAg
|
If at the end a number is left over then write it as a remainder
Factor Theorem
The (x ± p) is generally a factor of the polynomial and the factor theorem enables you to find this factor as it is rarely provided
The factor theorem states:
If f(x) is a polynomial and f(p) = 0 the (x - p) is a factor of f(x)
This enables you to factorise a cubic.
The factor theorem states:
If f(x) is a polynomial and f(p) = 0 the (x - p) is a factor of f(x)
This enables you to factorise a cubic.
In an exam you need to find out 'p' through trial and error until the value brings it to 0. Remember p can be +ve and -ve
To factorise the cubic fully divide the cubic by the factor found which will give a quadratic.
This can then be further factorised giving three sets of brackets normally.
Also if f(x) is a polynomial and f(b/a)=0 then (ax + b) is a factor
To factorise the cubic fully divide the cubic by the factor found which will give a quadratic.
This can then be further factorised giving three sets of brackets normally.
Also if f(x) is a polynomial and f(b/a)=0 then (ax + b) is a factor
Remainder Theorem
To find the remainder without using long devision (or to check the long devision) you can use the remainder theorem
The remainder theorem states:
If a polynomial f(x) is divided by (ax - b) then the remainder is f(b/a)
The remainder theorem states:
If a polynomial f(x) is divided by (ax - b) then the remainder is f(b/a)